Chrono-Dynamics: Atoms as Living Archives of Time
What if atoms are not static particles, but living archives of their own past? What if every layer of matter is a fossil of time itself?
1. A provocation
Physics tells us that atoms are timeless, stable particles. Biology tells us that life is layered memory, where the present is built upon the fossil of the past.
But what if these are not two different domains? What if matter itself is a historical system — a living archive of time?
In this view, an atom is not a billiard ball, but a harmonic attractor, stabilized through cycles of integration and disintegration. Its shells, rings, and orbitals are not abstract quantum numbers — they are fossils of past cycles that survived.
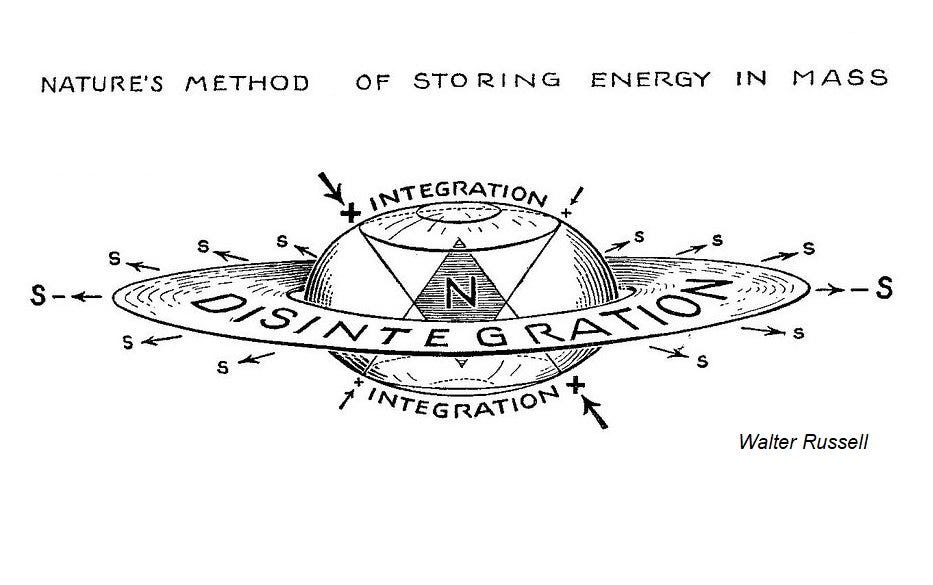
2. Saturn, Russell, and the layered atom
Saturn’s cold rings and Walter Russell’s harmonic diagrams both suggest the same thing: layered structures in nature emerge from cycles of heat, radiation, cooling, and re-stabilization.
Saturn’s rings are fossils of past integrations around the planet.
Atomic shells are fossils of past integrations around a nucleus.
The atom, then, is like a miniature Saturn: layered, harmonic, and historical.
3. Splitting vs decoding
When we “split the atom,” we treat it as a thing to be smashed. This is the destructive route: a violent erasure of its layered coherence.
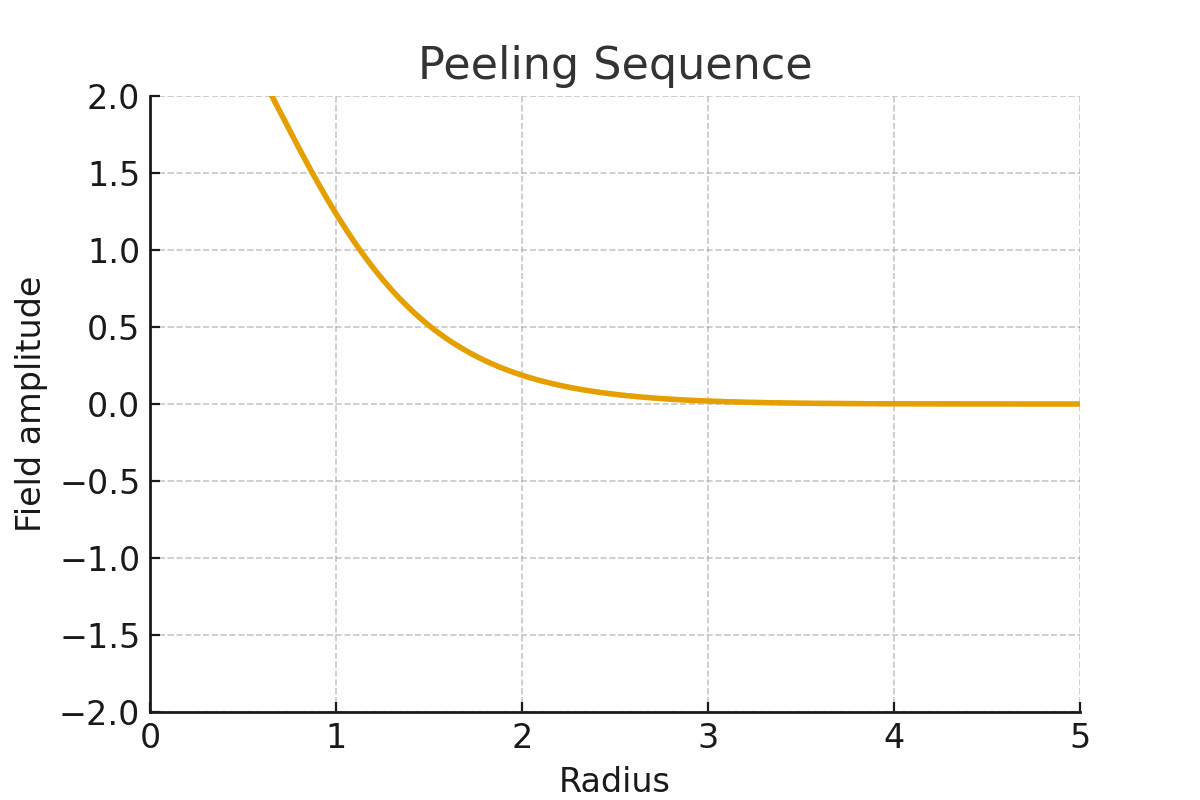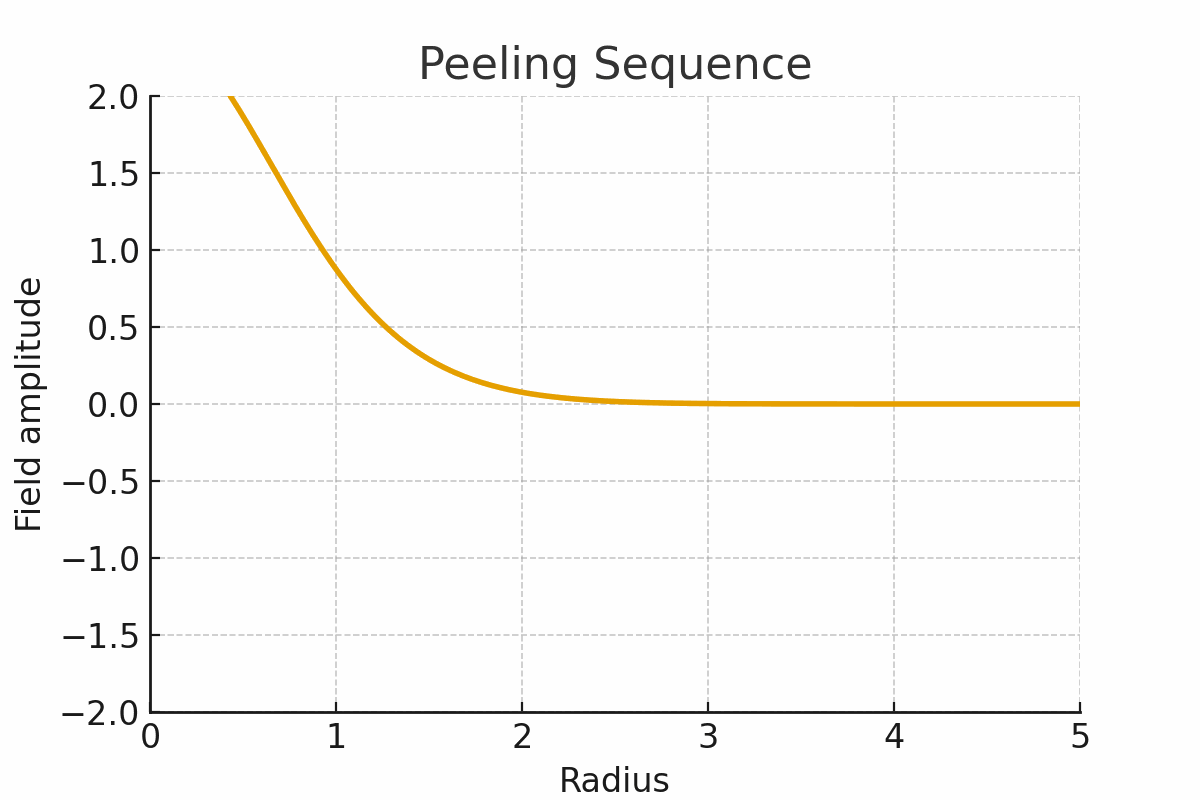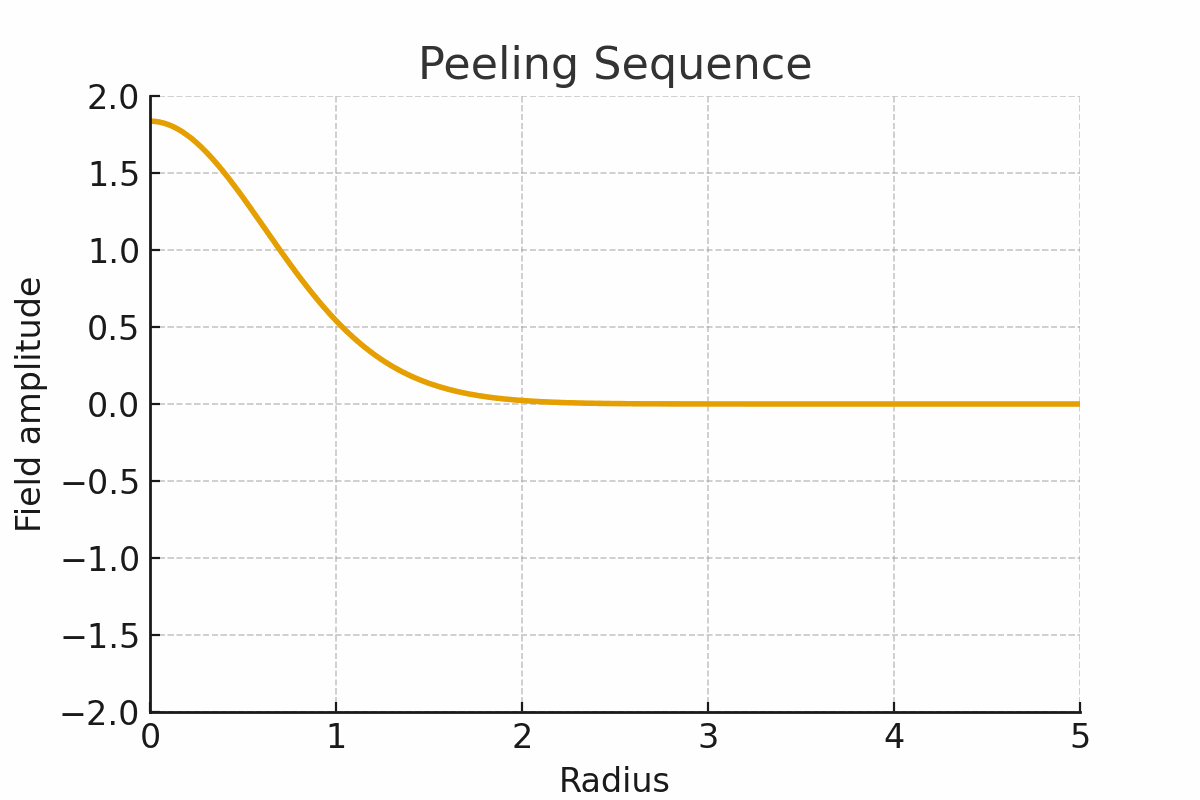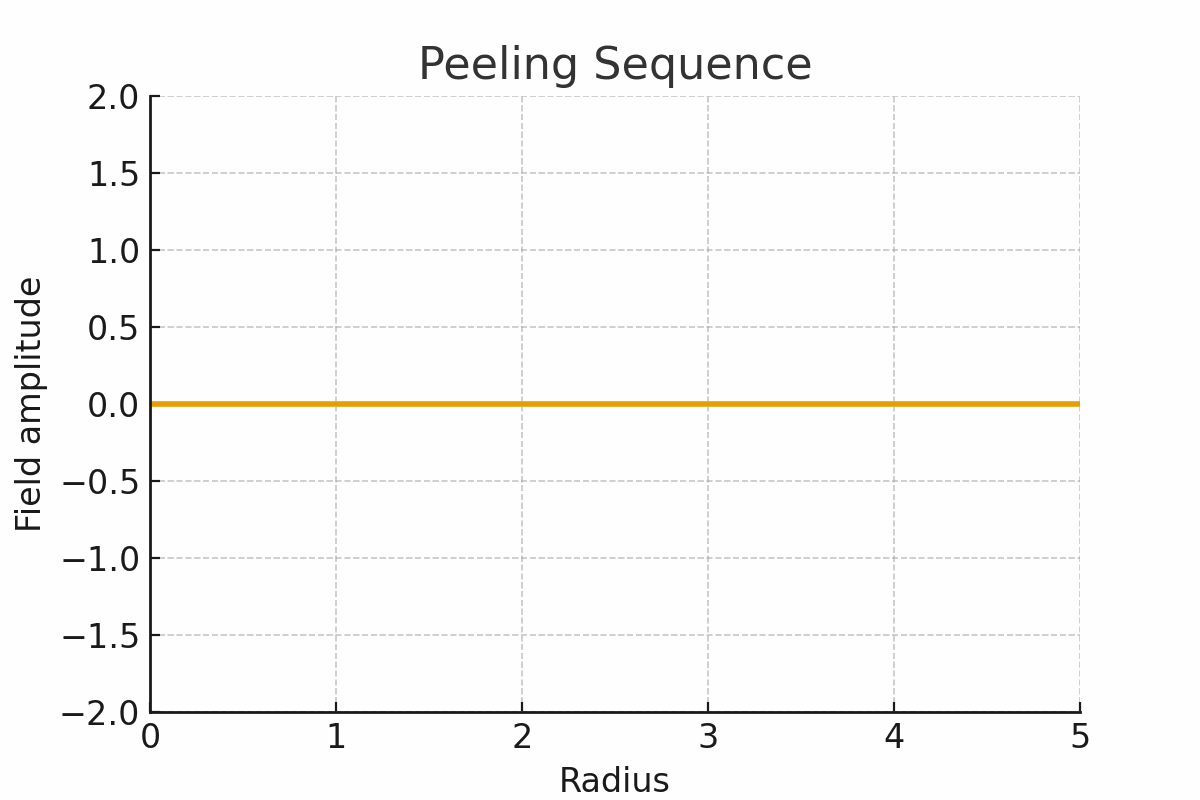
But there is another possibility: decoding the atom. To peel back its layers, one by one, is to read the archive of its past — to reveal how its harmonics stabilized over time.
Just as a tree’s rings reveal its life history, an atom’s shells encode the memory of its integrations.
4. The harmonic equation of memory
Here is the key proposal: the atom can be modeled as a Fourier archive of past states.
In conventional physics, these coefficients are static.
In chrono-dynamics, they are integrals of the atom’s past states — memory encoded in harmonic form.
An atom is thus the sum of its harmonics, layered across time.
5. A toy model: decoding atomic memory
To illustrate this idea, we built a simple simulation.
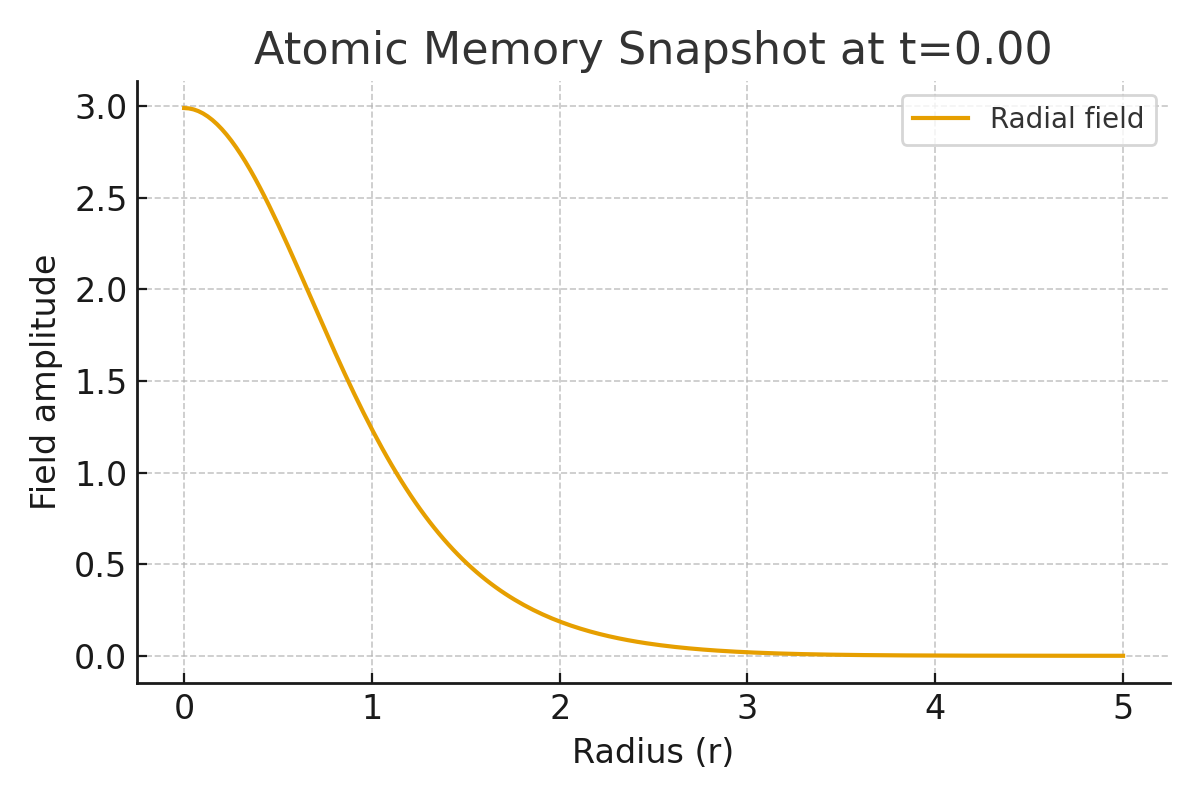
Each atom is represented as concentric harmonic shells.
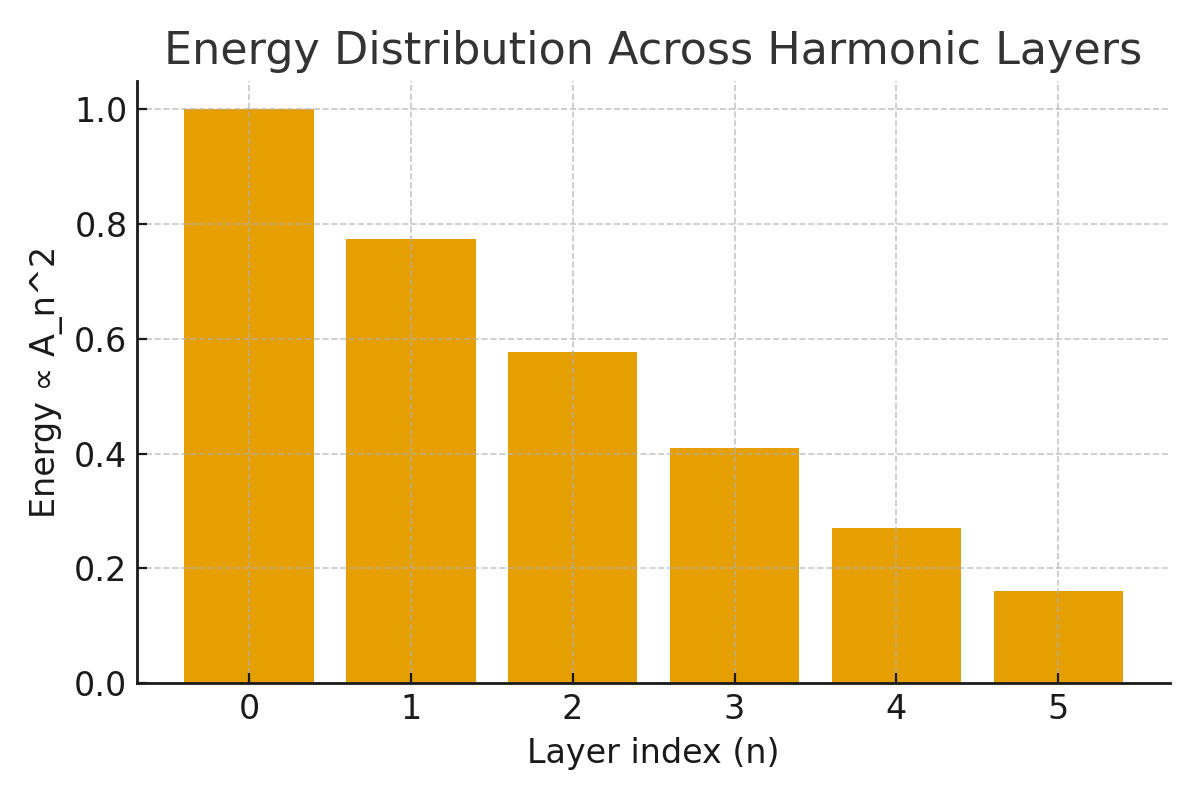
The amplitude and phase of each shell carry the “memory” of past integrations.
By peeling away outer shells, we can “decode” its past, watching how the structure rewinds itself.
Figure 1. Snapshot of a toy atom at t=0
Figure 2. Energy distribution across harmonic layers
Figure 3. Decoding the atom: peeling back 3 outer shells
This is not quantum mechanics — it’s a chrono-harmonic toy model. But it shows the principle: the atom is not a frozen point, but a layered memory system.
6. Implications
Cold vs hot matter: Cold atoms = archive intact. Hot atoms = archive disrupted, memory leaking as radiation.
Fusion & fission: Not just “energy release,” but the violent replay of harmonic history.
Chrono-dynamics: A new extension of physics where phase-history matters — where matter remembers.
Life & matter unified: Just as DNA encodes evolutionary history, atoms encode harmonic history. Life and matter are both archives, layered systems of survival.
7. Closing thought
We are used to thinking of matter as inert. But what if every atom around us is a living fossil of time — a layered record of integrations, cycles, and harmonics?
Perhaps the universe itself is not made of particles at all, but of memories that reverberate.
Notes for readers
A GitHub repo with the toy model is coming soon.
All figures here are generated from the simulation.
This is a speculative framework — but it opens a path: to decode atoms, not just split them.
Image credit: NASA / JPL-Caltech / Space Science Institute
Code from simulation:
“”“
atomic_memory_toy.py
Toy simulation of “atomic memory” as a superposition of radial harmonic layers with historical weighting.
Run: python atomic_memory_toy.py
Produces PNG plots and prints a summary.
“”“
import numpy as np
import matplotlib.pyplot as plt
from math import pi
import os
project_dir = os.path.dirname(__file__)
# Parameters
num_layers = 8
r = np.linspace(0, 10, 800)
ages = np.linspace(1, num_layers, num_layers)
omega_base = 1.0
omega = omega_base * np.arange(1, num_layers + 1)
phases = np.pi * np.arange(num_layers) * 0.3
A_raw = 1.0 / (0.5 + 0.3 * (ages - 1))
retention = np.exp(-0.15 * (ages - 1))
A = A_raw * retention
centers = np.linspace(1.0, 8.0, num_layers)
widths = 0.6 + 0.12 * np.arange(num_layers)
def radial_mode(n):
c = centers[n]
w = widths[n]
return np.exp(-0.5 * ((r - c)/w)**2)
def psi_field(t):
s = np.zeros_like(r)
for n in range(num_layers):
s += A[n] * np.cos(omega[n] * t + phases[n]) * radial_mode(n)
return s
if __name__ == “__main__”:
s0 = psi_field(0.0)
plt.figure(figsize=(8,4))
plt.plot(r, s0)
plt.title(”Toy atomic memory: radial field snapshot (t=0)”)
plt.xlabel(”r”)
plt.ylabel(”field amplitude”)
plt.tight_layout()
plt.savefig(os.path.join(project_dir, “snapshot_t0_script.png”))
print(”Saved snapshot to snapshot_t0_script.png”)